Formal Verification Of ML
Towards Provable Guarantees
Table of Contents
TL;DR
In the previous articles, we explored identifying the best-suited model for your use case through testing and benchmarking. But ask yourself: does testing and benchmarking give you the confidence to deploy these models in critical scenarios where a mistake is consequential? Do those 10,000 test cases provide you with everything you need? Perhaps you’re considering the scope and coverage of the testing and benchmarking or the inherent uncertainty that these models will face in their environment. This is precisely where formal verification moves beyond testing. It allows for a deeper analysis of the model itself, systematically searching for the fragilities that lead to failure. By generating concrete counterexamples, it proves where the model breaks, giving you the power to build a truly robust system before it's ever deployed.
Formal verification is not a new concept; it has long been integral to ensuring reliability in hardware and, to a lesser extent, software. According to Wikipedia, “formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property.” Immediately, four essential components emerge clearly from this definition:
System under verification: The specific hardware or software whose behaviour requires to be rigorously checked.
Formal specification: Precisely defined requirements or properties the system must satisfy, expressed mathematically rather than informal descriptions.
Correctness criterion: Conditions that confirm the system meets the specification or identify cases where it fails.
Formal methods: Mathematical techniques and proof engines employed to rigorously prove or disprove whether the system satisfies the given specification.
With these four components in mind, think of formal verification as moving beyond conventional testing by employing rigorous mathematical (formal) methods to provide stronger guarantees, which is particularly crucial when even small mistakes can lead to catastrophic outcomes, like in use cases like autonomous driving, medical diagnostics, security surveillance, malware detection, or high-stakes finance.
Formal verification has a long history in hardware dating back to 1984 with tools like Verilog and now SystemVerilog, tools standardised by IEEE and widely adopted for specifications for designing and verifying hardware. Software adoption lagged, largely due to state‑space explosion (as the number of state variables in the system increases, the size of the system state space grows exponentially). When dealing with software in aircraft or nuclear reactors, it's not enough to merely test a handful of scenarios. You need more guarantees that the software behaves correctly under every conceivable situation. Formal verification isn't merely theoretical but can have a practical, real-world impact. For example, it was successfully employed in the design of Paris’s autonomous Métro Line 14.

But how does this relate specifically to AI systems? The well-known AI researcher Andrej Karpathy highlights software evolution from Software 1.0 (manually written software) to Software 2.0 (software learning from data, ML models) and, more recently, Software 3.0 (AI-driven development).
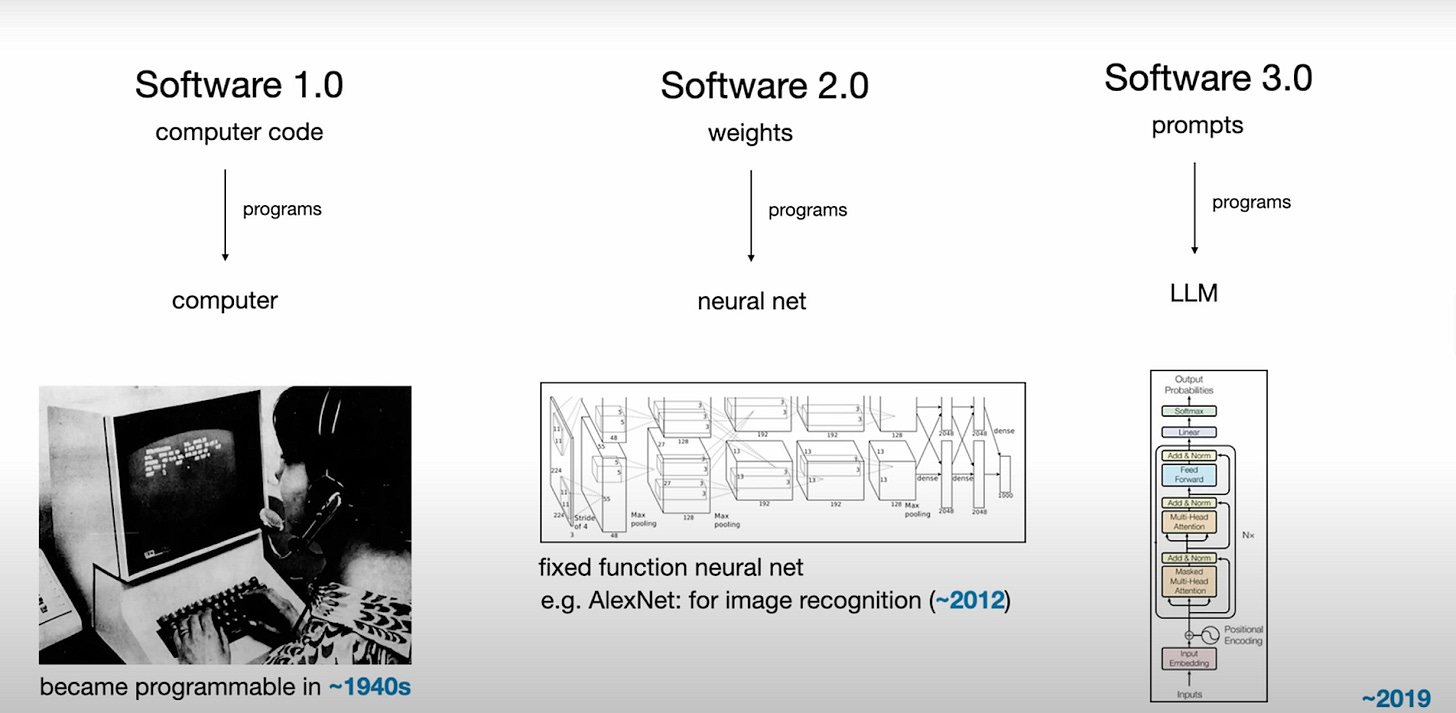
ML models, the core of Software 2.0, are now central to critical decision-making. However, their reliability is a key concern; while powerful, they are often fragile, failing in response to subtle data shifts that humans would not notice. This brittleness has serious consequences. For instance, minor data variations could lead to flawed loan approvals, while small visual distortions could cause an autonomous system to catastrophically misclassify its environment. Similarly, a critical customer service message could be misinterpreted by an NLP model, leading to significant service failures.
What do we want to verify?
These vulnerabilities (adversarial or otherwise) underscore the critical point that performance metrics and benchmarks alone aren't sufficient. We must rigorously verify specific model behaviours to eliminate these fragilities and blind spots. When failures can cost lives, livelihoods, or vast sums of money, “correctness” must be stated in precise, verifiable terms. The properties most often formalised in such critical systems include, but are not limited to, the following:
Robustness: Does the model maintain stable outputs despite minor perturbations in inputs?
Safety: Can we confidently say the model avoids catastrophic decisions under all possible conditions?
Fairness: Could subtle biases or irrelevant data variations lead to unfair outcomes?
Consistency: The model must uphold fundamental domain rules, ensuring its outputs never violate basic logical or physical constraints across all valid inputs.
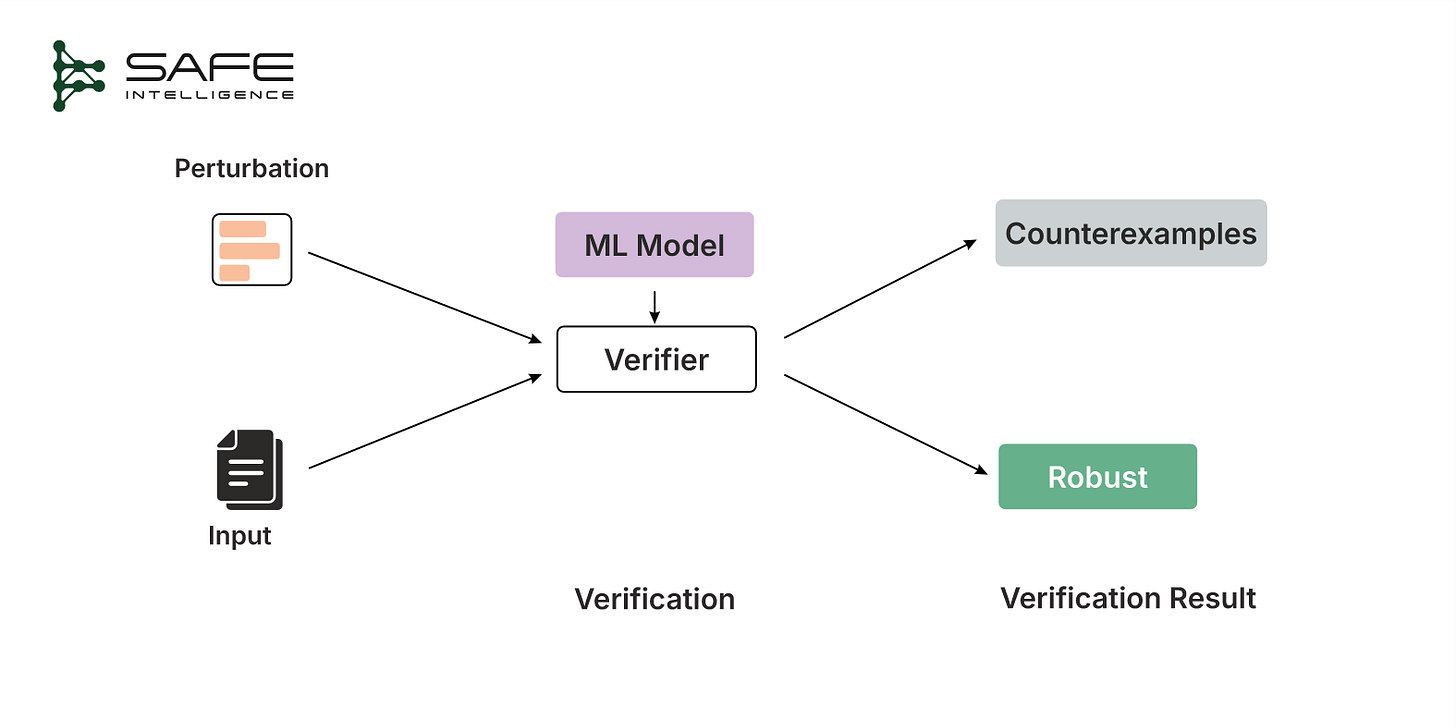
These are the types of behaviours formal verification methods are designed to assess, moving beyond intuition, testing and benchmarking. A quick overview of the verification process is illustrated below:
Verification Techniques
We’ve identified the critical properties, such as robustness, safety, fairness, and consistency, that we want our ML models to exhibit. Now, the next question is, how do we formulate these properties into a ‘verification problem’ that formal methods can solve? This involves translating the desired model behaviours into precise, mathematically checkable statements and then verifying whether the model satisfies these statements universally.
Formally speaking (no pun intended), the verification problem asks:
Given an ML model and a formal specification (a property like safety or robustness expressed in mathematics), does the ML model satisfy the formal specification for all admissible inputs and behaviours?
To solve this verification problem, we generally rely on two main techniques: constraint-based verification and abstraction-based verification.
Constraint-Based Verification
Constraint-based verification converts the verification problem, the input domain, model structure, and property to be checked into a single mathematical system of logical/optimisation constraints, typically fed to a Satisfiability Modulo Theories (SMT) or Mixed-Integer Linear Programming (MILP) engine. The solver treats this system of constraints as a single, complex puzzle. It doesn't check inputs one-by-one; instead, it uses powerful symbolic reasoning and logical deduction to intelligently prune away vast regions of the search space that cannot possibly contain a violation. Its goal is to find one concrete counterexample that satisfies every constraint at once.
Because this search explores all feasible sub-regions, the approach is sound (it never certifies a false property) and complete (it is guaranteed to find a counter-example if one exists). Given enough time and memory, the solver must terminate with either a proof that no violation exists or with a concrete counter-example that satisfies every constraint and therefore constitutes a genuine failure of the property. The price for such exhaustive coverage is the computational cost, which is prohibitively expensive.
Abstraction-Based Verification
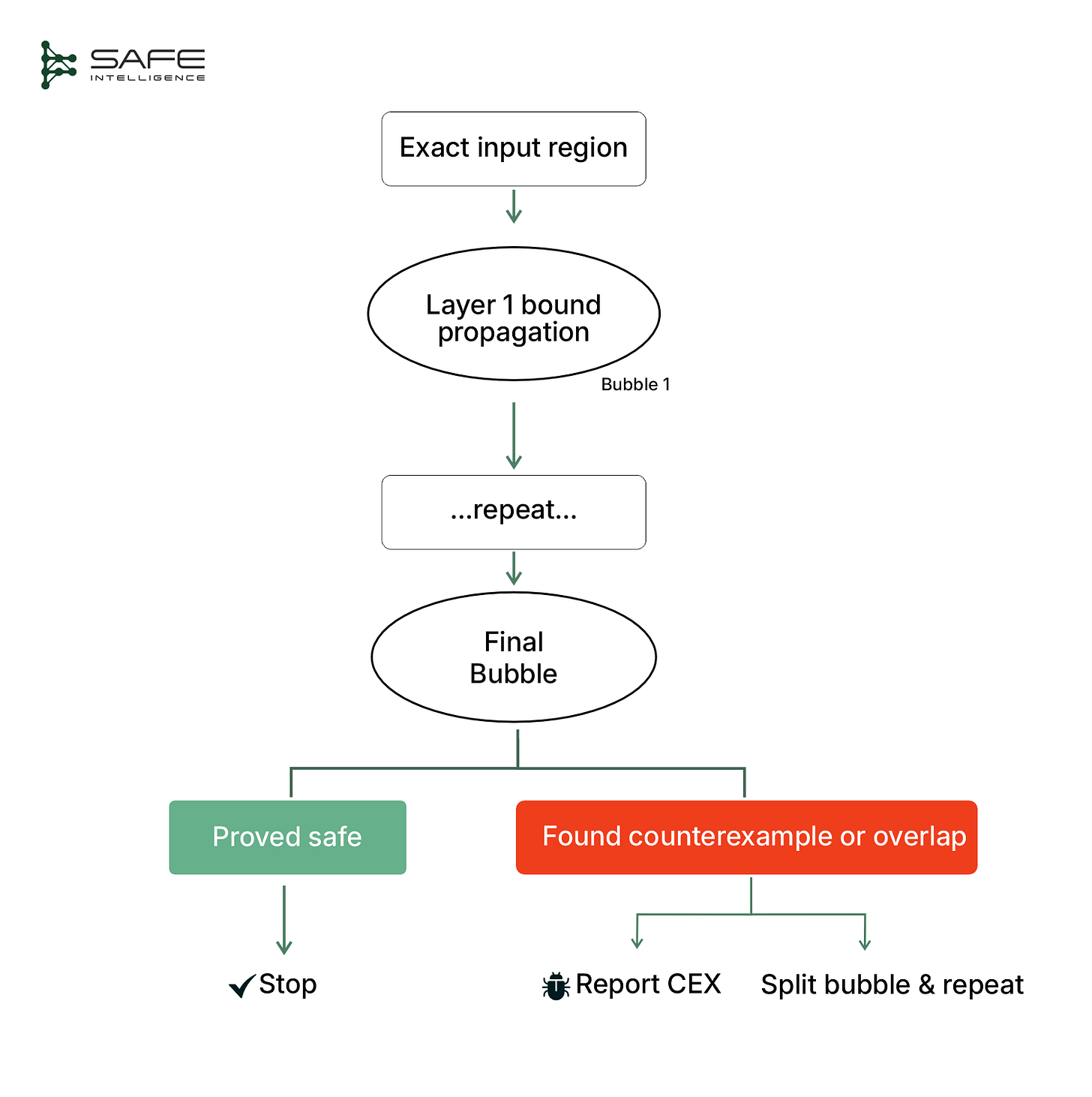
Abstraction-based verification trades theoretical completeness for speed and scalability. In other words, it is sound, but it is incomplete (it may stop with “unknown” even though the property is either true or false), especially if it runs out of time or memory. Unlike constraint-based verification, which pushes the exact verification problem into a heavyweight solver, abstraction-based verification takes a lighter, step-by-step route. It watches the input set flow through the model structure (such as layers in a neural net or splits in a decision tree), and after each layer or decision point, wraps all the possible outputs in one slightly oversized “bubble” (which can take different shapes, such as a box, polyhedron, or zonotope). This step-by-step process, also known as bound propagation, produces an over-approximation at every stage, ensuring every real behaviour is safely enclosed within these bubbles. If the final bubble never touches the danger zone, the model is provably safe; if it does touch, the method refines the bubbles or reports “unknown.”
This "bubble" approach has two main advantages. First, it's significantly faster and more scalable than constraint-based verification, because following one bubble at each stage is much simpler than exhaustively checking millions of individual inputs. Second, it provides trustworthy guarantees: if the final bubble sits fully in the safe region, the model is proven safe. However, since each bubble is padded for safety (over-approximated), it can sometimes become too large and overlap the unsafe zone. When this happens, the method can't immediately tell if there's a real problem or just extra padding. At this point, abstraction-based methods usually employ lightweight solvers to quickly determine whether a genuine violation exists within the bubble. If no violation is found, the bubble is refined by splitting the input region further. If time or resources run out before a clear answer is obtained, the method returns "unknown."
Comparison of Verification Techniques
Constraint-based and abstraction-based methods answer the same fundamental question: “Does my model always satisfy the given property?” However, their mathematical approaches differ significantly. To illustrate this clearly, let's first consider a concise comparative overview:
To vividly demonstrate these differences, let's trace how each one tackles a simple verification problem. Consider this tiny neural network and a safety property:
Layer 0 (input): x ∈ [0,1]
Layer 1 (linear): z = 2x − 1
Layer 2 (ReLU): h = max(0, z)
Layer 3 (output): y = −h + 0.8
Safety propery: y > 0 (for every x in [0,1])The property claims the network's output is always positive. Is this true? Let’s see how the two verification methods handle this.
For constraint-based verification, its steps include:
Constraint-based methods exhaustively explore possibilities to find definitive answers but face scalability limitations with complex or large models.
For abstraction-based verification, its steps include:
The abstraction-based approach delivers speed and scalability by making safe estimates. While its initial findings can be imprecise, its ability to iteratively refine its focus makes it a powerful and practical tool for verifying large-scale systems.
The Elephant in the Room: Does it Scale?
The critical question always arises when discussing formal methods: Does it scale?
Historically, these techniques have carried a reputation for being powerful but difficult to scale, often seen as best suited for academic exercises or smaller models. This is a valid concern based on the field's origins.
But that is no longer the full story. This exact scaling challenge is what our team at Safe Intelligence has been dedicated to solving. By developing novel approaches that blend mathematical rigor with computational efficiency, we are making scalable verification a reality for the complex, production-grade AI systems being deployed today.
Putting Formal Verification to Work
Applying these advanced verification techniques enhances the reliability and safety of ML models in critical applications now. As you embark on your AI assurance journey, these are the core principles to guide you:
Go Beyond Testing. Testing confirms behavior for inputs you've checked; formal verification proves correctness for entire classes of inputs you haven't, providing a far stronger guarantee of safety.
Precisely Define Correctness. The foundation of meaningful verification is translating business needs into mathematical properties. Whether it's robustness, fairness, or consistency, a clear specification is essential.
Verify Systems, Not Just Models. Compositional verification analyzes the complete system (the training data, the software environment, and its deployment dynamics) to build genuinely trustworthy AI.
The era of treating ML verification as a purely academic pursuit is over. These techniques have matured and are already being applied to solve real-world safety and reliability challenges at scale. This isn't a theoretical future, it's happening now.
In our upcoming articles, we’ll explore real-world case studies and practical applications that are helping make AI safer and more trustworthy across industries. But first, in the next article, we’ll show how we deploy these formally validated models in real systems. Stay tuned and stay safe.






I am loving these reads. Quite revealing!!
Interesting and insightful